Noise Analysis for Image Forensics
People seem to be liking Forensically. I enjoy hacking on it. So upgraded it with a new tool - noise analysis. I also updated the help page and implemented histogram equalization for the magnifier/ELA.
Noise Analysis
The basic idea behind this tool is very simple. Natural images are full of noise. When they are modified this often leaves visible traces in the noise in an image. But seeing the noise in an image can be hard. This is where the new tool in forensically comes in. It takes a very simple noise reduction filter (a separable Median Filter) and reverses it's results. Rather than removing the noise it removes the rest of the image.
One of the benefits of this tool is that it can recognize modifications like Airbrushing, Warps, Deforms, transformed clones that the aclone detection and error level analysis might not catch.
Please be aware that this is still a work in progress.
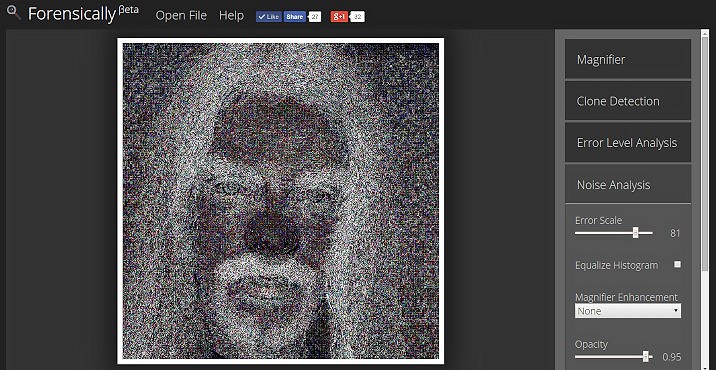
Example
Enough talk, let me show you an example. I gave myself a nosejob with the warp tool in gimp, just for you.

As you can see the effect is relatively subtle. Not so the traces it leaves in the noise!

The resampling done by the warp tool looses some of the high frequency noise, creating a black halo around the region.
Can you find any anomalies in the demo image using noise analysis?
A bit of code
I guess that many of the readers of this blog are fellow coders and hackers. So here is a cool hack for you. I found this in some old sorting code I wrote for a programming competition but I don't remember where I had it from originally. In order to make the median filter fast we need a fast way to find the median of three variables. A stupidly slow way to go about this could look like that:
// super slow
[a, b, c].sort()[1]Now the obvious way to optimize this would be to transform it into a bunch of ifs. That's going to be faster. But can we do even better? Can we do it without branching?
// fast
let max = Math.max(Math.max(a,b),c),
min = Math.min(Math.min(a,b),c),
// the max and the min value cancel out because of the xor, the median remains
median = a^b^c^max^min;
Mina and max can be computed without branching on most if not all cpu architectures. I didn't check how it's handled in javascript engines. But I can show you that the second approach is ~100x faster with this little benchmark.