I made myself a guitar tuner
I first learned about the fourier transform at about the same time I started to play guitar. So obviously the first idea that came to my mind at that time was to build a tuner to tune my new guitar. While I eventually got it to work the accuracy was terrible so it never ended up seeing the light of the day.
Fast forward a bit over a decade. It’s 2020 and we are fighting a global pandemic using social distancing. I obviously tried to find ways to directly address the issue with code but in the end there is only so much that can be done on that front and a lot of really clever people on it already.
So rather than coming up with another well intended but flawed design of a mechanical ventilator I decided to revisit this old project of mine. :)
So what’s in it?
The tuner has been built with a whole lot of web tech like getUserMedia to access the microphone, WebAudio to get access to the audio data from the microphone as well as web workers to make it a bit faster. Framework wise I used React and TypeScript.
With that out of the way, the rest of the article will focus on the algorithm that makes the whole thing tick.
Disclaimer
In the following sections I will oversimplify a lot of things for the sake of accessibility and brevity.
If you already have a solid understanding of subject please excuse my oversimplifications.
If you don’t keep in mind that there is a lot more to learn and understand than what I will touch on in this description.
If you want to go deeper I highly recommend reading the papers by Philip McLeod et al. mentioned at the end. They formed the basis of this tuner.
Going beyond the fourier transform
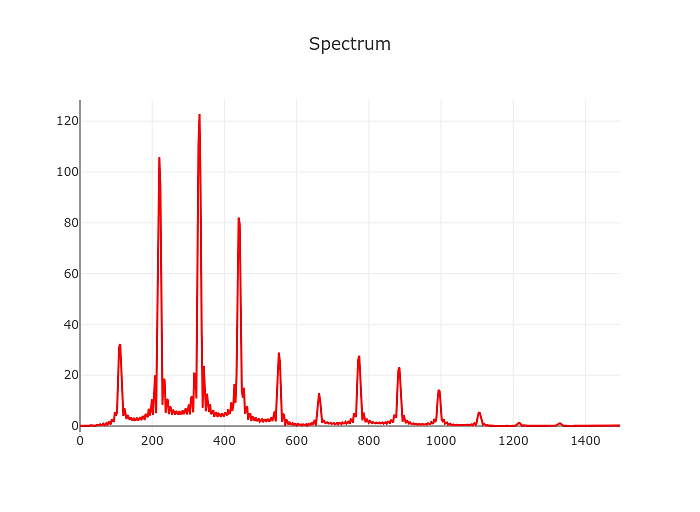
Initially I decided to resume this project from where I stopped years ago, by doing a straight fourier transform on the input and then selecting the first significant peak (by magnitude).
Not quite up to speed with the fourier transform? But what is the Fourier Transform? A visual introduction. is a video beautifully illustrating it.
The naive spectrum approach of course still works as badly as it did back then. In slightly oversimplified terms the frequency resolution of the discrete short-time fourier transform is sample rate divided by window size.
So taking a realistic sample rate of 48000 Hz and a (comparably large) window size of 8192 samples we arrive at a frequency resolution of about 6 Hz.
The low E of a guitar in standard tuning is at ~82 Hz. Add 6 Hz and you are already past F.
We need at least 10x that to build something resembling a tuner. In practice we should aim for a resolution of approximately 1 cent or about 100x the resolution we’d get from the straight fourier transform aproach.
There are approaches to improve the accuracy of this approach a bit, in fact we’ll meet one of them a bit later on in a different context. For now let’s focus on something a bit simpler.
Auto correlation
Compared to the fourier transform autocorrelation is fairly simple to explain. In essence it’s a measure of how similar a signal is to a shifted version of itself. This nicely reflect the frequency, or rather period of the signal we are trying to determine.
In a bit more concrete terms it’s the product of the signal and a time shifted version of the signal. In simplistic Javascript that could look a bit like this:
function autoCorrelation(signal) {
const output = [];
for(let lag = 0; lag < signal.length; lag++) {
for(let i = 0; i + lag < signal.length; i++) {
output[lag] += signal[i]*signal[i+lag]
}
}
return output;
}
The result will look a bit like this:
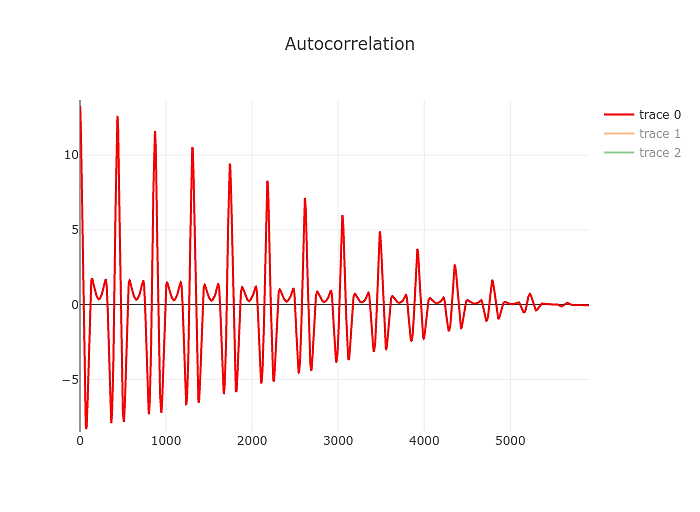
Just by eyeballing it you can tell that it’s going to be easier to find the first significant of the autocorrelation compared to the spectrum yielded by the fourier transform above. Our resolution also changed a bit, this time we are measuring the period of the signal. Our resolution is limited by the sample rate of the signal. So to take the example above the period of a 82 Hz signal is 48000/82 or 585 samples. Being off by a sample we’d end up at 82.19 Hz. Not great but at least it’s still an E. At higher frequencies things will start to look different of course but for our purposes that’s a good point to start.
The actual algorithm used in the tuner is based on McLeod, Philip & Wyvill, Geoff. (2005). A smarter way to find pitch. but the straight autocorrelation above is enough to understand what’s going on.
Picking a peak
Now that we have the graph above we’ll need a robust way of determining the first significant peak in it, which hopefully will also be the perceived fundamental frequency of the tone we are analysing.
We’ll do this in two steps, first we will find all the peaks after the initial zero crossing. We can do this by just looping over the signal and keeping track of the highest value we’ve seen and it’s offset. Once the current value drops bellow 0 we can add it to the list of peaks and reset our maximum.
From this list we’ll now pick the first peak which is bigger than the highest peak multiplied by some tolerance factor like 0.9.
At this point we have a basic tuner. It’s not very robust. It’s not very fast or accurate but it should work.
Improving accuracy
The autocorrelation algorithm mentioned above is evaluated at descrete steps matching the samples of the audio input, that limits our accuracy. We can easily improve on this a bit by interpolating. I use parabolic interpolation in my tuner.
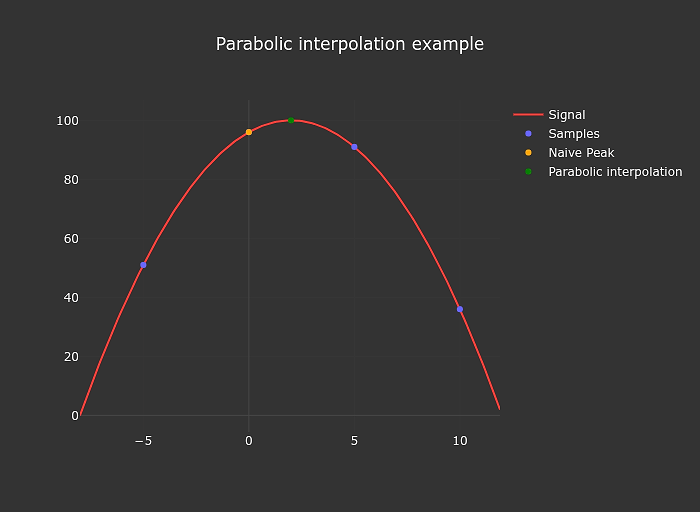
The implementation of this is also extremely simple
function parabolicPeakInterpolation(a, b, c) {
const denominator = a - 2 * b + c;
if (denominator === 0) return 0;
return (a - c) / denominator / 2;
}
Improving reliability
So far everything went smoothly. I had a reasonably accurate tuner for as long as I fed it a clean signal (electric guitar straight into a nice interface).
For some reason I also wanted to get this to work using much more dirty signals from something like a smartphone microphone.
At this stage I spend quite a bit of time implementing and evaluating various noise reduction techniques like simple filters and variations on spectral subtraction. In the end their main benefit was in being able to reduce 50/60 Hz hum but the results were still miserable.
So after banging my head against the wall for a little while I embraced a bit of a paradigm shift and gave up on trying to find a magical filter that would give me a clean signal to feed the pitch detection algorithm.
 Onset Locking
Onset Locking
I now use the brief moment right after the note has been plucked to get a decent initial guess of the note being played. This is possible because the initial attack fo the note is fairly loud resulting in a decent signal to noise ratio.
I then use this initial guess to limit the window in which I look for the peak in the auto correlation caused by the note and combine the various measurements using a simple kalman filter.
I named the scheme onset locking in my code, but I’m certain it’s not a new idea.
Making it fast
I hope the O(n²) loop in the auto correlation section made you cringe a bit.
Don’t do it that way. Both basic auto correlation and McLeods take on it (after applying a bit of basic algebra) can be accelerated using the fast fourier transform.
Good bye n squared, hello n log n. :)
Even with the relatively slow FFT implementation I’m using the speed up is between 10 and 100x. So the opimization is definitely worth doing in practice as well.
I’m also using web workers to get the calculations off the main thread and while at it also parallelized.
The result is that the tuner runs fast enough even on my aging Galaxy S7.
What is left to do
Performance in noisy environment is still bad. Using the microphone of a macbook the tuner barely works, if the fan spins up a bit too loudly it will fail completely.
I’d definitely like to improve this in the future but I also have the suspicion that it won’t be trivial, at least without making additional assumptions about the instrument being tuned.
Another front would be to add alternative tunings, and maybe even allow custom tunings. That should be relatively easy to do but I don’t currently have any use for it.
Further reading
McLeod, Philip & Wyvill, Geoff. (2005). A smarter way to find pitch.
McLeod, Philip (2008). Fast, Accurate Pitch Detection Tools for Music Analysis.

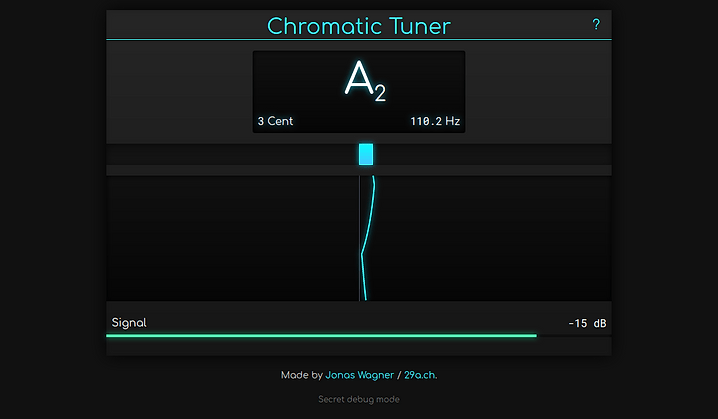 Try the chromatic tuner
Try the chromatic tuner